[데이터베이스] B+Tree, 해싱, 인덱싱 정리
학교 데이터베이스 수업을 들으면서 뒤로 갈수록 내용이 심화되고 좋은 정보도 많기에 글로 정리해보려고 한다!🤓🤓
Disk 구조

중요한 점은 File은 block단위로 디스크에 저장되고 메모리에 load 할 때는 page단위로 한다는 점이다. 그래서 block단위의 file들을 메모리에 가져올 때 transfer time이라는 비용이 발생한다. 이러한 transfer비용을 줄이기 위해서 cache가 등장한다.
이때, cache에서 read 할 땐 괜찮지만 update/delete 할 때는 디스크와의 동기화를 맞춰야 하는 게 중요하다.(db replication 할 때도 느꼈을 것이다)

이제 index를 보면 크게 두 가지로 나뉜다.
- unclustered Index : 엔트리 순서와 데이터 순서가 일치하지 않는다. ex) 전공 서적 같은 경우의 뒤 쪽 'INDEX(찾아보기)'
- clustered Index : 엔트리 순서와 데이터 순서가 일치한다. ex) 서적들의 앞 쪽에 있는 '차례'

10,000 pages가 있을 때, 100개의 row를 disk에서 찾으려고 한다. 이때 transfer page의 수는 page당 20개의 투플(row)을 찾을 수 있다. 이때, heap, sorted, unclustered, clustered일 때 몇 번 만에 찾을 수 있을 것인가.
- heap: 찾을 때마다 한 개씩 찾을 수 있으므로 10,000개 전부 뒤져봐야 한다. 정답 : 10,000번
- sorted: binarySearch를 하면 되기 때문에 log2(10,000)번 찾아보고, 반올림해서 14가 되므로 시작 페이지는 이미 찾았으니 4-5개이다. 정답 : log2(10,000)+4~5 -> 18~19번
- nuclustered: 정확히 page안에 찾는 row들이 꽉 차있으면(20개씩) 5번이면 끝나지만 최악으로 page안에 찾는 row가 1개씩 있으면 100 row를 찾기 위해서 100번 전부 뒤져야 한다. 정답 : 5~100번
- clustered: 찾는 페이지의 시작점이 찾는 row의 시작점과 딱 맞아떨어지면 5번이면 끝나지만(뒤로는 데이터가 순서대로 있기 때문에) 딱 안 맞아떨어지면 6번이 된다. 정답 : 5~6번
index파일은 데이터 파일과 분리해도 되고 안 해도 되는데분리하는 게 더 좋다. 왜냐하면 인덱스 파일과 데이터 파일이 같이 있으면 인덱스 파일을 load 할 때, 쓸데없는 데이터 파일도 같이 load 되기 때문이다.
따라서 분리해놓고 index file만 보고 data file이 있으면 그때 loading 하는 게 좋다.
B+Tree
일반적으로 노드에 data entry들은 차수(order)를 d라고 했을 때, d <= m(data entry) <=2d까지 들어갈 수 있다.

ISAM은 단말 노드를 제외한 인덱스 노드들의 구조가 고정되어 있다. 그래서 데이터가 한쪽으로 몰릴 수 있고, overflow chain이 발생할 수 있어서 안 좋다.
- 단말 노드에 삽입할 때, 단말 노드가 꽉 차있으면 copy를 한 후에 올려야 한다. (단말 노드에서는 데이터를 갖고 있어야 하므로)
- 단말 노드가 아닌 곳에서 승진할 때는 데이터가 아닌 index를 올리므로 copy 안 하고 바로 올려도 된다.
Insertion
두 가지 방법이 있다. 그중 1번 방식에 대해서 학교에서 배웠다.
- 삽입 들어온 걸 포함해서 그중 가운데를 승진한다.
- sibling 중 빈 곳에 넣고 부모 노드도 수정 + 복사 승진한다.
만약 중복되게 들어오면, Rid(Page, slot 조합)를 통해 중복을 구분한다. ex) <a, Rid> a는 attribute search key이다.
Deleting
- 지운다.
- entry >= d, 그냥 지우면 된다. 끝
- entry = d-1, ( 지우면 50%가 안될 때)
- 주변 sibling에서 가져온다.
- 안되면 합병, 부모 index 없앤다. / root가 부모일 때는 root 포함해서 부모 노드를 만든다.
비 단말 레벨에서 엔트리를 재분배하지 않는 것이 좋다.
Prefix Key Compression
검색 능력 향상을 위한 키 압축을 할 때는 왼쪽 서브 트리의 가장 큰 값과 오른쪽 서브트리의 가장 작은 값을 비교해서 기준 잡고 압축해야 한다.
Bulk Loading of B+Tree

- 데이터 entry들 정렬
- root로 사용할 하나의 empty page 할당 후 첫 번째 Page에 대한 포인터 삽입
- 정렬된 데이터 entry의 각 page에 대해 entry하나씩 root page에 추가.

Hashing(해싱)
대부분의 상용 데이터베이스는 해싱보다는 B+Tree를 사용한다.
- 해싱은 range selection이 안된다.(데이터가 연속되어 있지 않기 때문에)
- 해싱은 '조인'과 같은 관계형 연산을 구하는데 tree보다 효과적이다.
Static Hashing(정적 해싱)

- overflow 발생 가능(해시 값이 같을 수 있기 때문에)
- overflow chain 줄이기 위해 M을 키우면 된다. (M은 버켓의 수이다)
- 동시적 접근 측면에서 좋다.
- 하지만 버켓의 수가 고정되어 있다.
Extendible Hashing(확장성 해싱) - 동적 해싱(dynamic Hashing)
- directory를 사용한다.
- 따라서 overflow chain(overflow page)이 없다.
- Global depth of directory: 버켓 엔트리에 속한 최대 비트의 수
- Local depth of directory: 버켓에 속한 엔트리를 구별하기 위한 비트의 수
Insertion

- 버켓이 full, split 한다.
- 만약 버켓이 꽉 차면 디렉토리를 더블링 한다.
- GLOBAL DEPTH는 최소 비트 개수를 보는 것이다. LOCAL DEPTH <= GLOBAL DEPTH
Directory Doubling 하는 방법에는 2가지가 있다. 이건 그림으로 보는 게 이해하기 훨씬 쉽다.
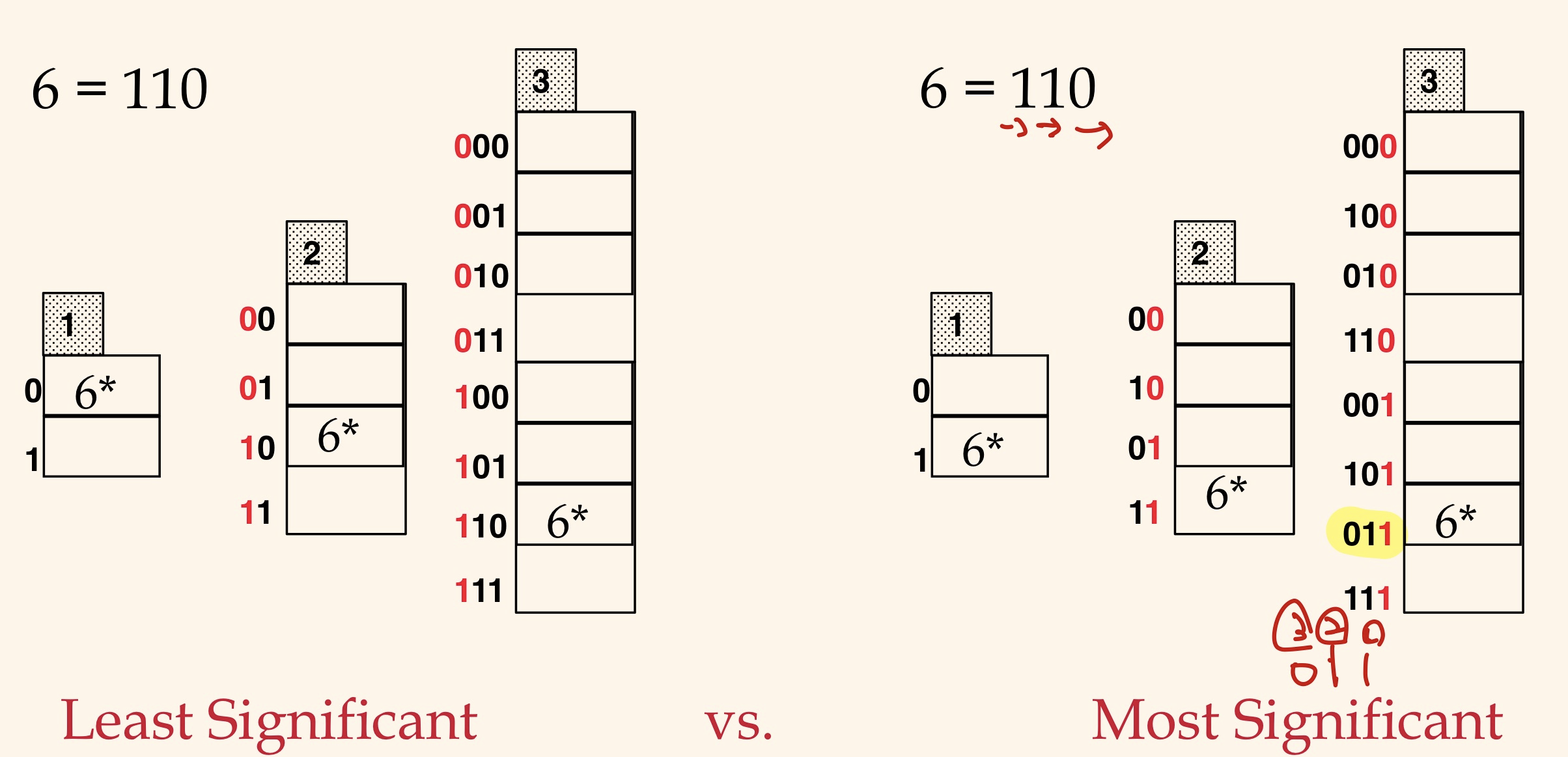
Linear Hashing(선형 해싱) - 동적 해싱(dynamic Hashing)


h0 함수로 해싱을 진행하고 분할하면 h1 함수로 해싱을 진행하고 계속 해싱 함수가 변해간다.
- 여러 level의 hash function 사용
- 디렉토리를 사용하지 않는다. 버켓을 키워나간다.
- 충돌을 다룬다.
- 데이터 분포가 편중되어 있으면 overflow chain으로 인해 성능이 저하된다.
- round robin방식을 사용한다.
- overflow chain이 2를 넘지는 못한다고 한다.
- Round 단위로 split 되고, 현재 round의 숫자를 Level이라고 한다.
- N(level)은 버켓의 수이다. ex) N(0) = 4, N(1) = 8
Insertion
해시 함수 h(level+1)은 이 버켓(b)의 분할에 의해 생겨난 버켓의 번호는 b+N(level)이다.
- overflow가 발생하지 않으면 Next는 그대로 있고 삽입만 일어난다. 분할도 안 일어난다.
- 어디서 overflow가 발생하든 분할이 일어날 때마다 Next가 가리키는 버켓을 분할하고 분할한 후에는 Next+1 한다.
- Next이전은 h(level+1)적용되있고, 이후는 h(level)을 적용해본다. b+N(level)은 h(level+1)이 적용되어있다.
- Next가 가리키는 곳에서 삽입이 되어 버켓이 넘쳐서 분할 해야하면 overflow chain안 만들고 분할만 하고 Next+1
- Next == N(level) -1 이면, h(level)을 전부 다 돌면 level+1, Next = 0으로 초기화한다.
한눈에 보기 정적 해싱 vs 확장 해싱 vs 선형 해싱
- 정적은 directory(x), overflow(o)
- 확장은 directory(o), overflow x
- 선형은 directory(x), overflow(o) - overflow 개수 최대 2 정도로 적음